Desde su origen, la humanidad ha tratado de entender la Tierra, cual es su composición, forma y como se mueve. el desarrollo de sistemas de medición ha sido fundamental para satisfacer estas inquietudes y algunas ocasiones tales como tales mediciones se han hecho de manera ingeniosa y creativa. Medir consiste en encontrar la proporción existente entre un objeto y una unidad de medida. Por ejemplo, utilizamos una regla para medir las longitudes. Pero en ocasiones no es posible aplicar la unidad de medida de forma directa, y cuando esto sucede, se pueden medir algunas dimensiones para calcular indirectamente otras que queremos obtener. 

Erastones de Cirene fue un sabio griego que estuvo a cargo de la biblioteca de Alejandría a mediados del siglo tercero antes de nuestro tiempo, es decir, hace 2249 años. Ademas de Astronomía estudio otras disciplinas como Geografía, Filosofía y Poesía y se dice que era muy inteligente por lo que sus contemporáneos le llamaban beta ¡ERA EL SEGUNDO MEJOR EN TODO LO QUE HACIA!!
A Erastones se le atribuye la invención de la esfera armilar: un instrumento formado por anillos metálicos que giran con diferentes velocidades alrededor de un centro común. En el tiempo de Eratóstenes se pensaba que la Tierra estaba en el centro de un sistema de esferas, en las que se encontraban el Sol, la Luna, los planetas y las estrellas fijas. La esfera armilar permitía calcular con buena exactitud el movimiento de los astros como se observa desde la Tierra.El ángulo A que forma la longitud de la sombra en Alejandría permite deducir el ángulo B que forma con Siena (A=B=7º), ya que una recta que corte a dos paralelas tiene iguales ángulos alternos interiores (en este caso 7º de los 360 del círculo terrestre)

“Sobre la medición de la Tierra” es el título de la obra de Eratóstenes donde se describe un gran logro de la imaginación y de la creatividad científica, que ha sentado algunas bases para los métodos científicos modernos de la Geografía. El contenido de su obra lo sabemos por las citas de autores clásicos, puesto que lo escrito por él no sobrevivió hasta la actualidad. Único hombre en preguntarse cuál era la circunferencia de la Tierra, otro experimento con una metodología muy similar, aunque menos conocido, fue llevado a cabo por Yi Xing hace unos 1300 años, ¡1000 años después de la medición de Eratóstenes! Este sabio envió 13 equipos de medición a diferentes ciudades de China para que midieran la sombra que producía una vara de bambú en el verano y en invierno, y logró calcular con gran precisión la longitud de un segmento del arco meridiano. 
En la actualidad, la medición directa o indirecta de muchas de las características de la Tierra se llevan a cabo dentro de disciplinas como la Geodesia, la Geografía, la Geología y la Geofísica.

Eratóstenes entonces realizó las mismas observaciones en Alejandría el mismo día a la misma hora, descubriendo que la luz del Sol incidía verticalmente en un pozo de agua el mismo día a la misma hora. Asumió de manera correcta que si el Sol se encontraba a gran distancia, sus rayos al alcanzar la tierra debían llegar en forma paralela, si esta era plana como se creía en aquellas épocas, y no se deberían encontrar diferencias entre las sombras proyectadas por los objetos a la misma hora del mismo día, independientemente de donde se encontraran.

Sin embargo, al demostrarse que si lo hacían (la sombra dejada por la torre de Siena formaba 7 grados con la vertical), dedujo que la tierra no era plana y, utilizando la distancia conocida entre las dos ciudades y el ángulo medido de las sombras, calculó la circunferencia de la tierra en aproximadamente 250.000 estadios (unos 40.000 kilómetros, bastante exacto para la época y sus recursos).

DISTINTAS FORMAS DE MEDIR LA TIERRA 

1.- MEDICIÓN DE LA TIERRA CON EL SOL

Medir la longitud de la Tierra mediante pasos parece utópico, pues, aunque se pudiera realizar tal medición a través del océano, el error acumulado paso a paso sería al final de gran magnitud. Pero, alguien, hace milenios, consiguió tomar una pequeña muestra de la superficie terrestre y calcular su longitud total con admirable precisión:

Se trata del griego alejandrino Eratóstenes, que en el año 240 antes de Cristo, pudo medir la longitud del meridiano terrestre entre las ciudades de Siena y Alejandría, y mediante cálculos geométricos establecer que la circunferencia de la Tierra era de 40.000 Km.. Sorprende tal precisión, pues en la actualidad se sabe que la Tierra mide en la zona ecuatorial 40.076 Km., es decir, Eratóstenes tuvo un error de sólo un 0,18%.

La forma en que Eratóstenes consiguió tal prodigio merece unos cuantos párrafos, comenzando por una breve biografía de esta mente inquieta de la antigüedad:

Eratóstenes era un científico que vivía en la ciudad egipcia de Alejandría. Los más envidiosos le llamaban Beta (la “segunda” letra de alfabeto griego) en alusión a que era “segundo” mejor en todo, pero en realidad Eratóstenes era Alfa, porque era el primero en todo lo que se proponía; de hecho fue historiador, astrónomo, geógrafo, poeta, filósofo, matemático, crítico teatral..

Siendo director de la Biblioteca de Alejandría, leyó un día que en Siena, mucho más al Norte próximo a la primera catarata del Nilo, un palo vertical no proyectaba sombra a las doce del mediodía del 21 de julio, es decir que los rayos del Sol caían directamente sobre las cabezas; este hecho era constatable viendo cómo el Sol podía verse perfectamente reflejado en el fondo de un pozo.

Para cualquier otra persona ese dato pasaría inadvertido, pero Eratóstenes tenía la mentalidad de un inquieto hombre de ciencia. Observaba cómo durante el solsticio de verano, a medida que avanzaban las horas, las sombras que proyectaban las columnas del templo acortaban su longitud. Se propuso entonces realizar el experimento de saber si en Alejandría un palo vertical proyectaba sombra, y descubrió que sí. Tras preguntarse por qué lo hacía en Alejandría y no en Siena, la única respuesta que encontró fue que la superficie de la Tierra estaba curvada.

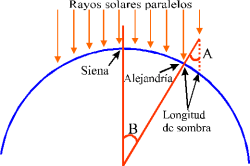
Eratóstenes pudo saber por la inclinación de la sombra proyectada en Alejandría, que el ángulo que formaba con Siena era de 7 grados, es decir la cincuentava parte de los 360 grados de una circunferencia. Se le ocurrió entonces contratar a un hombre para que midiera paso a paso la distancia entre Alejandría y Siena, y no fue una simple excursión, porque Eratóstenes averiguó que ambas poblaciones distaban 800 kilómetros entre sí. Con estos datos pudo deducir la circunferencia de la Tierra: 800 Km. x  50 = 40.000 Km. Sin duda, esto constituye un logro grandioso para los elementos de que disponía Eratóstenes hace más de 2.000 años, pues su error de cálculo era prácticamente despreciable, y sin utilizar metro ni GPS.

2.- MEDICION DE LA TIERRA CON FIGURAS GEOMETRICAS 
Medir el tamaño de la Tierra es tan fácil como contar las tajadas de una pizza. Vemos como. Supongamos que queremos medir la circunferencia de la pizza que aparece en la foto:

 Para medir el perímetro de la pizza la cortamos en tajadas, medimos que tan largo es el borde de una de las tajadas y multiplicamos esa longitud por el número de tajadas. Eso es todo! Bueno iguales hacemos con la Tierra. El diagrama que aparece abajo representa la circunferencia de la Tierra y la tajada formada por dos ciudades: Washington y Cali. 

 

Como ves, el diagrama de la Tierra es como el de la pizza. Entonces medimos la circunferencia de la Tierra tal como se midió la pizza: formamos una tajada usando las dos ciudades (Cali y Washington), estimamos que tan largo es el borde de la tajada (es decir la distancia Cali-Washington), contamos el número de tajadas que pueden salir, y finalmente, la circunferencia de la Tierra es igual a el número de tajadas multiplicado por la distancia Cali-Washington. Antes de poder llegar a la respuesta final nos quedan dos cálculos importantes por hacer: el número de tajadas y la distancia Cali-Washington. Si conocemos el ángulo de la tajada (representado con la letra ‘c’ en el diagrama) podemos calcular muy fácilmente el número de tajadas en las que podemos dividir la Tierra, ya que sabemos que el ángulo total de un círculo es de 360°. Entonces el número de tajadas es: Numero de tajadas = 360°/c

 Pero, ¿Qué es el ángulo ‘c’? Este es el ángulo de la tajada (ver diagrama) y para calcular este ángulo vamos a usar las mediciones de la sombra y el palo. Vas a medir los ángulos ‘a’ y ‘b’ (ver diagrama) con un transportador directamente sobre un dibujo de un triangulo rectángulo formado por la sombra (base del triangulo) y el palo (lado perpendicular a la base). Puedes dibujar este triangulo sobre papel a escala (por ejemplo dividiendo el largo del palo y de la sombra por un factor de 10). Entonces el ángulo de la tajada ‘c’ es simplemente la diferencia a – b (el diagrama al final muestra la geometría y la relación entre estos ángulos). El último dato que nos falta es la distancia entre las dos ciudades. Para esto vas a medir la distancia con una regla directamente sobre un mapa. Luego conviertes la distancia a kilómetros midiendo la escala que aparece en el mapa. El cálculo final del tamaño de la Tierra es:

 Circunferencia = (numero de tajadas) x (distancia Cali-Washington) La relación entre los ángulos ‘a’, ‘b’ y ‘c’ se puede apreciar en el diagrama: 

3.-COMO MEDIR LA TIERRA CON FORMULAS MATEMATICAS 

La estimación que hizo Eratóstenes del radio de la Tierra fue, sencillamente, genial. Partiendo de que la Tierra tenía forma de esfera, los rayos solares inciden al mediodía en las ciudades de Alejandría y Syene
La longitud de un arco y el ángulo que encierra son magnitudes directamente proporcionales. Por tanto, la razón entre dos ángulos es igual a la razón entre las distancias (longitudes de arco). Así, teniendo en cuenta que cuando se da la vuelta al planeta giramos 360º y recorremos la longitud de un círculo del mismo radio:
CÁLCULO DEL RADIO DE LA TIERRA
¿cómo midió la distancia entre las ciudades: 902 km?
Formula matemática para medir el radio de la tierra 
De la manera más elemental: le encargó a alguien que fuese de una ciudad a otra andando en línea recta (o lo más recta posible) y que contase los pasos. Originalmente, la distancia se midió en “estadios”, es decir, la longitud del estadio de Olimpia, ya que entonces no existía la unidad del “metro”. El “medidor” dijo recorrer, aproximadamente, 5000 estadios. Sabiendo que el estadio medía 185 m de longitud, se tiene obtienen los 902 km.